How to create a memory recall machine.
TotalRecall
We have an idea of creating new mathematical methods and models to better understand and manipulate complex real world scenarios.The Q* concepts--Time-Space Splitting and Quantum Computing:The idea of splitting time and space into distinct equations that can randomly flip like qubits aligns to quantum computing. Quantum computers use qubits, which can represent both 0 and 1 simultaneously, and they are being explored for their potential to solve complex problems more efficiently.Blockchain and Time Stamping:Datanacci.blockchain," uses blockchain technology to record and timestamp events, and accompanied granular data locators. Blockchain's distributed ledger and cryptographic properties are used to secure and verify the time and sequence of events.Mathematical Modeling:Developing mathematical equations to model real world scenarios requires expertise in mathematics, particularly in areas like probability theory, quantum mechanics, and cryptography. Datanacci works with with experts in these fields to create appropriate models.Interdisciplinary Collaboration:Given the complexity of these concepts, it is beneficial to collaborate with experts from various knowledge domains, including mathematics, physics, computer science, and blockchain technology. Interdisciplinary collaboration will help refine and validate the concept.Practical Applications:Let's consider the practical applications and real-world problems that our mathematical models could address. Identifying specific use cases will guide work and help determine the relevance and effectiveness of the model.Testing and Validation:Any new mathematical model or method undergo rigorous testing and validation to ensure the accuracy and reliability in solving problems. Simulation and data science experimentation is always necessary.Resources and Tools:Based on the complexities of the mathematical modeling and simulations, we leverage and have access to powerful computational resources and datanacci sdk and software tools.Sampling / Snapshot and environment focus. We need to figure out a way to snapshot to such a degree were their is data sufficiency to support recreating the captured environment, at various levels of "replay" granularity requested.In summary, developing a working equation or mathematical model for such a concept is a significant undertaking that requires a deep understanding of multiple domains and collaboration with experts. It's a challenging but exciting endeavor that could have far-reaching implications in fields like cryptography, data security, and quantum computing. We are building a team of experts and researchers to explore and develop this concept further. Send us a note below to apply.can complement and enhance mathematical processes and applications in several ways:Proof Verification: Blockchain can be used to verify mathematical proofs and theorems. When a mathematician or researcher develops a complex proof, it can be recorded on the blockchain, providing a tamper-resistant and immutable record of the proof's validity. This can enhance trust in mathematical results.Timestamping: Blockchain's timestamping capabilities can help establish the chronology of mathematical discoveries and research. Researchers can timestamp their work on the blockchain to prove when a particular theorem or equation was first developed, which can be crucial in establishing intellectual property rights.Data Integrity: Blockchain's data integrity features can ensure that mathematical data and calculations remain unchanged over time. This is particularly useful in scientific research where data integrity is critical.Decentralized Collaboration: Blockchain can facilitate decentralized collaboration among mathematicians and researchers. Smart contracts on blockchain platforms can automate the distribution of research grants, royalties, and funding based on predefined criteria, making collaboration more efficient.Mathematical Libraries: Blockchain can be used to create decentralized mathematical libraries where researchers can access and contribute to mathematical knowledge. These libraries can use smart contracts to reward contributors and ensure the authenticity of published work.Secure Cryptography: Blockchain technology is rooted in advanced cryptographic techniques. These cryptographic principles are often used in various branches of mathematics, including number theory and abstract algebra. Blockchain's secure cryptographic foundation can be leveraged in mathematical research and applications.Tokenization of Mathematical Assets: Researchers can tokenize mathematical assets such as patents, algorithms, or research papers on blockchain platforms. This can enable the trading and transfer of mathematical assets in a transparent and secure manner.Mathematical Data Marketplaces: Blockchain can support the creation of mathematical data marketplaces where mathematicians and researchers can buy and sell datasets, algorithms, and research findings. Smart contracts can automate transactions and ensure fair compensation.Verifiable Randomness: Blockchain can provide a source of verifiable randomness, which is essential in some areas of mathematics, cryptography, and computer science.Decentralized Computing: Blockchain networks can be used for decentralized computing, enabling researchers to harness the computational power of distributed nodes for complex mathematical calculations and simulations.While blockchain has the potential to revolutionize aspects of mathematical research, it's important to note that it is not a replacement for traditional mathematical methods and techniques. Instead, blockchain can serve as a valuable tool for enhancing transparency, collaboration, and the integrity of mathematical research and applications. Researchers and mathematicians are exploring these possibilities, and the intersection of blockchain and mathematics continues to evolve.
our blockchain can complement and enhance mathematical processes and applications in several ways:Proof Verification: Blockchain can be used to verify mathematical proofs and theorems. When a mathematician or researcher develops a complex proof, it can be recorded on the blockchain, providing a tamper-resistant and immutable record of the proof's validity. This can enhance trust in mathematical results.Timestamping: Blockchain's timestamping capabilities can help establish the chronology of mathematical discoveries and research. Researchers can timestamp their work on the blockchain to prove when a particular theorem or equation was first developed, which can be crucial in establishing intellectual property rights.Data Integrity: Blockchain's data integrity features can ensure that mathematical data and calculations remain unchanged over time. This is particularly useful in scientific research where data integrity is critical.Decentralized Collaboration: Blockchain can facilitate decentralized collaboration among mathematicians and researchers. Smart contracts on blockchain platforms can automate the distribution of research grants, royalties, and funding based on predefined criteria, making collaboration more efficient.Mathematical Libraries: Blockchain can be used to create decentralized mathematical libraries where researchers can access and contribute to mathematical knowledge. These libraries can use smart contracts to reward contributors and ensure the authenticity of published work.Secure Cryptography: Blockchain technology is rooted in advanced cryptographic techniques. These cryptographic principles are often used in various branches of mathematics, including number theory and abstract algebra. Blockchain's secure cryptographic foundation can be leveraged in mathematical research and applications.Tokenization of Mathematical Assets: Researchers can tokenize mathematical assets such as patents, algorithms, or research papers on blockchain platforms. This can enable the trading and transfer of mathematical assets in a transparent and secure manner.Mathematical Data Marketplaces: Blockchain can support the creation of mathematical data marketplaces where mathematicians and researchers can buy and sell datasets, algorithms, and research findings. Smart contracts can automate transactions and ensure fair compensation.Verifiable Randomness: Blockchain can provide a source of verifiable randomness, which is essential in some areas of mathematics, cryptography, and computer science.Decentralized Computing: Blockchain networks can be used for decentralized computing, enabling researchers to harness the computational power of distributed nodes for complex mathematical calculations and simulations.While blockchain has the potential to revolutionize aspects of mathematical research, it's important to note that it is not a replacement for traditional mathematical methods and techniques. Instead, blockchain can serve as a valuable tool for enhancing transparency, collaboration, and the integrity of mathematical research and applications. Researchers and mathematicians are exploring these possibilities, and the intersection of blockchain and mathematics continues to evolve.
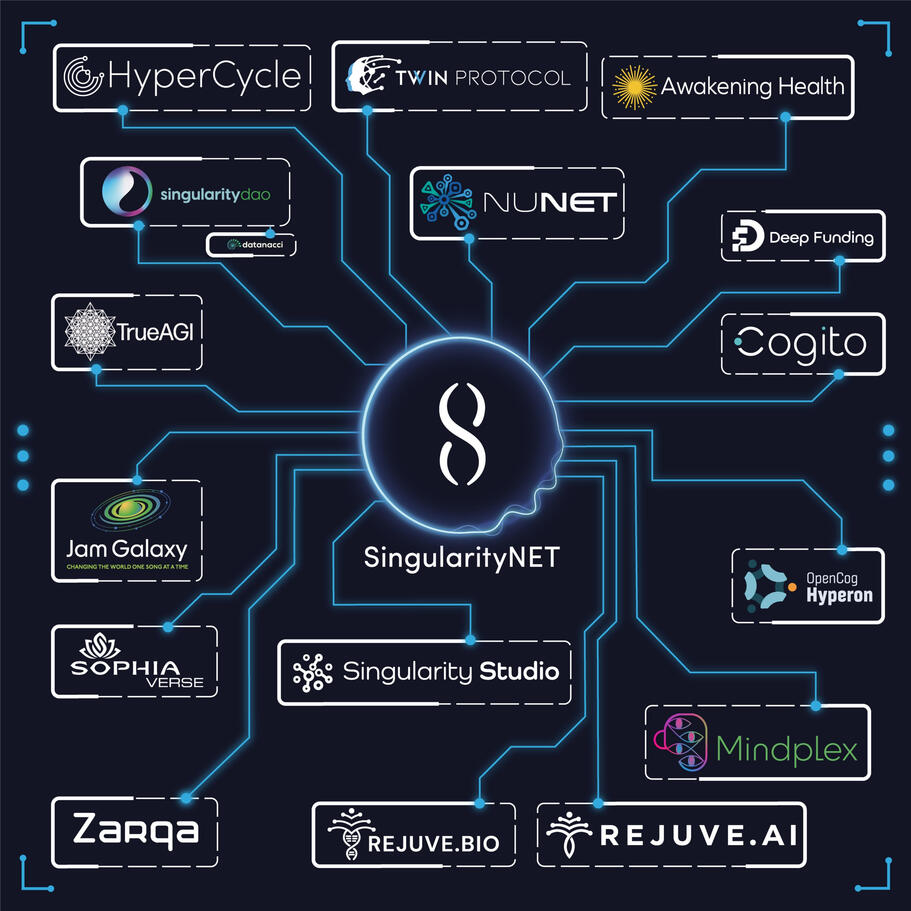
Our Projects: Datanacci.blockchain, Datanacci.dao, Datanacci.agi, SungularityNet, Twinprotocol, rejuve.ai, Skinswap.world, Inspiredby.Fun.
Datanacci AI
Contact us
We will be launching a new verson of our platform which will run copleatly on the singlarityNet and https://www.twinprotocol.com/ versions soon! keep in contact by subscribing to our mail list. we will only contact you with platform news and evernts. Your security is most important. We will not share your email.